Conservation equations of fluid flow

This article discusses the absolute fundamental equations that dictate how things flow in pipes, and therefore, form the basis of all of my modelling

Houskeeping

Before discussing any form of mathematical modelling, we must first understand that we need as many equations as there are unknowns. If there are 5 'things' unknown about a system, then we must have 5 equations. Any more and we over-constrain the system, and so not all of the equations (potentially) can be satisfied. Any fewer and we are under-constrained, that is, there aren't enough equations to find a unique value for each variable.

Note that I am not saying that if you have as many equations as variables, you will certainly find a solution. Just that, without the same number, you aren't guaranteed a good answer. Necessary but not sufficient.

We begin with the concept of 'Control Volume'. This is the fundamental unit of analysis in the field of thermofluids. A control volume is nothing more than a region of space, usually of finite volume (as opposed to an infinitesimal or infinite region) that we are interested in. It might be the inside of a water pipe, for example, or a sliver of air just above the outer edge of an aircraft wing. We analyse such volumes in the same way as when we draw a Free-Body Diagram in structural analysis; we specify and then balance the different elements flowing into or out of the region. A control volume has a boundary that we call a control surface, which may or may not be a real, tangible thing.

Now, in the most general case, the control volume would be a three-dimensional object. Often, however, the conduits we use are symmetric around an axis, and we can assume that the major changes to a fluid property happen along the direction of flow, and the change along the transverse direction are much smaller. This way, we can average the properties at each cross section, leading to a one-dimensional flow assumption. We could even go a step further and just assume the whole conduit is one property, leading to the 'Lumped' assumption. In most of my work, I use a 1D assumption, because it is good enough, while still being simple enough to let me run complex systems.

We next need to understand that, in thermodynamics, when we are dealing with a pure or pseudo-pure substance, if we know the values of two independent properties of the substance, we can calculate all the other properties. That is, if we know pressure and density, for example, we can now calculate the enthalpy, internal energy, the temperature, the viscosity, the surface tension and all the rest of it. Similarly, if we know pressure and enthalpy, or density and internal energy, we can calculate the other stuff. If we are calculating saturation properties, then just one property is enough. So, for a given pressure of a liquid, there is a unique saturation temperature, a unique density etc.

This, however, is not the full story. Knowing the thermodynamic state of a fluid does not give us any fluid dynamic information. In other words, we are still missing the 'flow' properties. In other words still, we are missing knowledge of the flow rate of the substance. This might be in the form of velocity (m/s), the volumetric flow rate (L/s) or mass flow rate (kg/s).

So what we have now are three unknowns. Conversely, if we can figure out these three unknowns, we can figure out everything about the control volume in question. Thus, we are looking for three equations to do the trick.

Reynold's transport theorem

I want to highlight a feature of control volumes that may not be immediately obvious from the past few paragraphs. A control volume does not have to be stationary. It is not essential that the control volume stay in place while fluid flows in and out of it. We could have a control volume that flows at precisely the speed of the fluid, and thus, it is as if we have chosen our favourite bit of the fluid, and are following it around as it flows through the system, and seeing what happens to it.

In fact, this method of analysis has a name for it. It's called the Lagrangian approach. The alternative, where the control volume is fixed and fluid flows in and out, is called the Eulerian approach.

Neither of these is better or worse than the other, but instead are suited for different tasks. More importantly, we helpfully have a way to convert between the two approaches using an identity called the Reynold's Transport Theorem.

If we have an Extensive property^[1] Y, then the intensive version of the property is \(\frac{dy}{dM}\). The Reynold's transport theorem states that

\[\frac{dY_{system}}{dt} = \frac{\partial}{\partial t}\left( \iiint_{CV} y\rho dV\right) + \iint_{CS} y.\rho \left( \vec{v}.d\vec{S}\right)\]

This is a rather complex looking equation, and deriving it is also non trivial, but understanding the intuition of it is rather simple.

Let's say you have a system with fluid flowing in a closed loop. Now, the left side of the equation measures the change over time of any extensive property (let's say system energy). Then, this equation is merely stating that any change in the total energy of the system (the left hand side) can be caused either by a change in the internal energy of the system (say you had a lots of drag along a wall generating heat), or energy crossing the 'control surface' (say a heater heating up the fluid).

That's it. That's all the governing equations say. That we cannot have phantom generation or destruction of conserved quantities such as mass or energy.

The left hand side in Equation 1 above is the Lagrangian approach, while the right hand side is the Eulerian approach. The Reynold's transport theorem gives us a way to relate the two.

The three governing equations that we deal with basically take the form of the equation above, where we change 'Y' to the correct property. Let's look at them one by one.

Conservation of mass

This equation states that mass can neither be created nor destroyed. Although CERN does destroy mass often, this is not a problem on the scale of thermodynamics that we are dealing with. For our purposes, mass is a fixed thing.

To find the format of the equation, we substitute Y as mass (M) in the equation above. But, mass is fixed, therefore, \(\frac{dM}{dt}=0\). Also, y (aka "mass per unit mass") is just 1. Then, the governing equation of mass is:

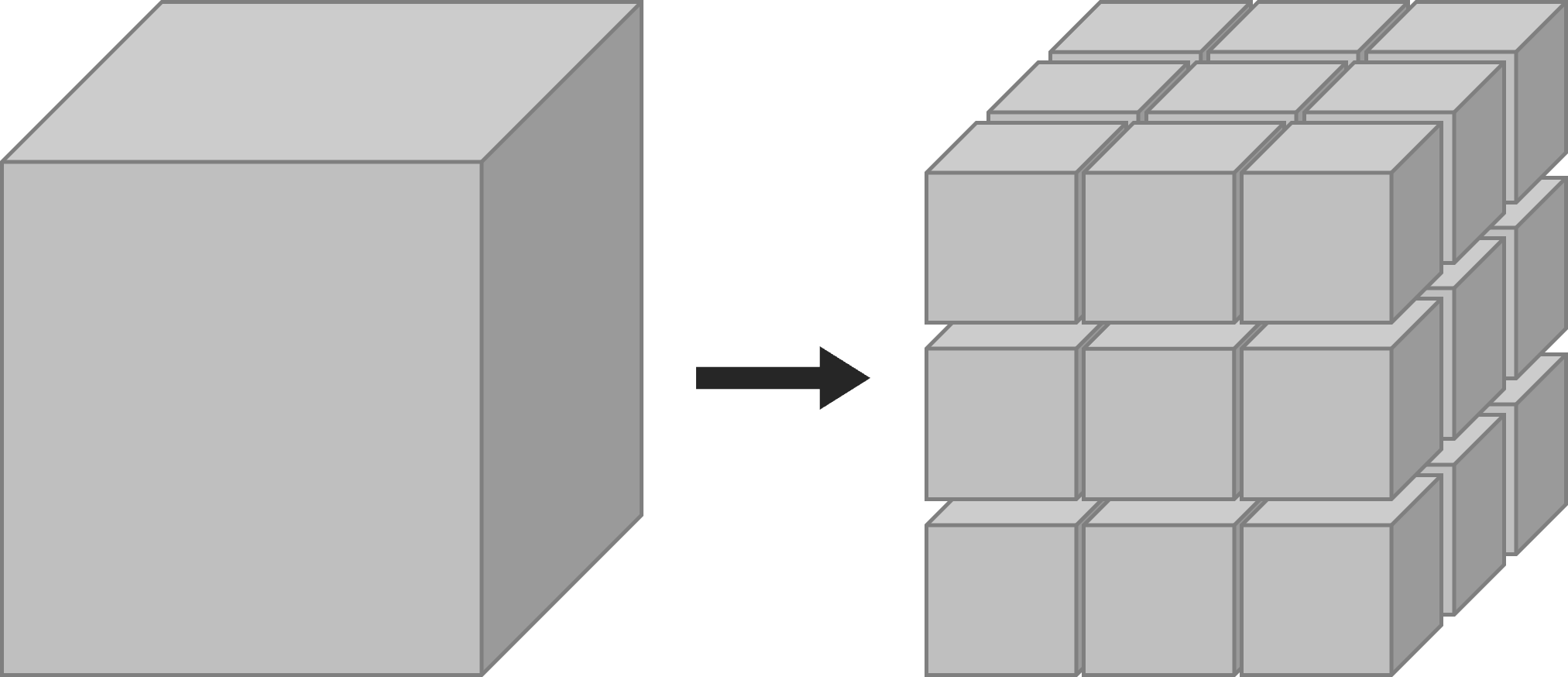
\[\frac{\partial}{\partial t}\left( \iiint_{CV} \rho dV\right) + \iint_{CS} \rho \left( \vec{v}.d\vec{S}\right) = 0\]

I want to stop and point out one thing here. Those integral signs. Let's say we have a cube. Now, instead of assuming that the fluid properties (say density) is constant in the whole region, we could chop up the cube into smaller segments, and then sum up the properties for each segment. For example, say we divide the cube into 3 pieces along each side. This gives us 27 smaller cubes. Calculating the average properties of 27 small cubes gives us a better approximation than 1 large cube. By making these 27 cubes into 64, 125, 216, 343 etc., we can get better and better approximations. The integral sign just indicates the idea of infinitely many 'discretizations'.

Now, we have the intuition down for the equation, but in the current format, it's not easy to implement, so let's alter that. Let's first assume that our pipe is circular. This isn't required, it just makes things easier for me to talk about. Now, I make the assumption that I talked about earlier; that the flow properties mainly change along the direction of flow. This allows me to assume axisymmetry, that is, we average the properties at across the cross-section.

Now, we make some simplifications. The Control Surface we were talking about is now just the inlet and the outlet port because those are the only two places where flow can come in or out. Then, the \(\iint_{CS} \rho \left( \vec{v}.d\vec{S}\right)\) becomes \(\dot{m}_{in}-\dot{m}_{out}\), because the flow can't come in through the surface.

Next, about that triple (volume) integral \(\frac{\partial}{\partial t}\left( \iiint_{CV} \rho dV\right)\), two of those dimensions cease to be of interest to us, because of the aforementioned axisymmetry. Therefore, this becomes \(\frac{\partial}{\partial t}\left(A. \int_{x} \rho dx\right)\).

Then, our simplified equation now looks like:

\[\frac{\partial}{\partial t}\left(A. \int_{x} \rho dx\right) + \dot{m}_{in}-\dot{m}_{out} = 0\]

Excellent.

Momentum equation

The most general form of the momentum equation is called the Navier-Stokes equation. Or, at least, that is what we were taught^[1]. It seems that it is more proper to collectively call all of the governing equations dictating viscous flow the Navier-Stokes equations. These equations hold a mystical place in the annals of Physics, what with them being one of the Millennium Prize Problems. But our purposes here are a lot more utilitarian.

The momentum equation starts out life as Newton's Second Law of Motion, aka \(Force = Mass \times Acceleration\). If taken instantaneously, this equation can be thought of as: an instantaneous change in Force causes an instantaneous change in the product of mass and acceleration.

Let's look at the right hand side of the equation first. Acceleration is the rate of change of velocity over time, aka \(d\vec{v}/dt\). Therefore, the right hand side of the equation is then the rate of change of (Mass * Velocity), aka the rate of change of momentum.

Effectively, if we flip the way we think of the equation around, we might say that if there is a net force on the control volume, it will cause a change in the momentum of the fluid.

\[\frac{D}{Dt}\left(m\vec{v}\right)=\Sigma\vec{F}\]

Now, if we take our first equation and substitute momentum, aka \(m\vec{v}\) for our do-it-all variable 'Y', we get

\[ \frac{D}{Dt} \left(m\vec{v}\right) = \frac{\partial}{\partial t}\left( \iiint_{CV} \vec{v}\rho dV\right) + \iint_{CS} \vec{v}\rho \left( \vec{v}.d\vec{S}\right) \]

Again, the left hand side is the Lagrangian expression, aka if we were following a bit of fluid around and examining it's momentum change, while the right hand side is the Eulerian expression.

But, our momentum change is the net force, so that the equation of momentum will read:

\[ \Sigma \vec{F} = \frac{\partial}{\partial t}\left( \iiint_{CV} \vec{v}\rho dV\right) + \iint_{CS} \vec{v}\rho \left( \vec{v}.d\vec{S}\right) \]

We could do a similar simplification that we did for the mass balance equation. I won't do it here, mainly because it won't help in any further gaining of intuition. Instead, let's look at our final equation.

Conservation of energy

We know the method by now. Take our first equation, and substitute the variable of interest. In this case, no prizes for guessing, we substitute energy for our variable 'Y'.

\[\frac{D}{Dt}\left(E\right) = \frac{\partial}{\partial t}\left( \iiint_{CV} e\rho dV\right) + \iint_{CS} e\rho \left( \vec{v}.d\vec{S}\right) \]

This \(e\) here is the total energy of the fluid. The total energy is the sum of the internal energy (the jiggling energy of the molecules of fluid), plus the kinetic and potential energies.

Anyway, we now look at the first law of thermodynamics, which says that for a system, the change in energy is caused by the sum of any heat input/output from the system, plus any work done by or on the system.

\[\frac{D}{Dt}\left(E\right)=\Sigma\dot{Q} -\Sigma\dot{W} \]

The work component in the equation above is interesting, because work comes in many forms. First, what is work? It is Force times the displacement. Work can come in many forms. Things could move under a magnetic field, under an electric field. A shaft could stir things up, causing movement etc. For our purposes, we will neglect just about all these kinds of work. Our only concern is this thing called the pressure work.

Pressure-volume work

An object at rest continues to be at rest until acted upon by an external force. This statement is familiar to us. Now, let's take our pipe from before. As you see in the picture below, Johnny-come-lately Mr. Diagonal Hatching particle wants to enter the grey pipe. But the particles already in the pipe are resistant to move. Thus, to be able to enter the pipe, it needs to displace a region equivalent to it's own volume, which is shown as the cross hatching.

So, what is the work done by this volume? Well, again, work is force times displacement. Now, we know that pressure is force per unit area. Thus, force is pressure times the area. Also, the displacement here is the actual 'length' of this particle (dL in the figure).

Then, the work done is \(W_{PV}=P.A.dL = PV\)

You see this displaced volume as the Cross Hatching volume at the outlet. This is the origin of the pressure work, and this is the only one we will consider in this article. The figure above only considered the possibility of flow going into and out of the pipe via the inlet ports. But we could generalise this to a deformable control volume as well, where any deformation of the control surface would need some work done on it. For the moment, I consider a rigid volume, so let's forget about the deformability. Also, note that the equation above is work done, but the rate of work done (in the units of Power), would be \(P\dot{V}\), aka the rate of change of the volume.

Right, back to regularly scheduled programming. We now substitute our PV work and our heat transfer into the energy balance equation.

\[ \Sigma\dot{Q}-P\dot{V} = \frac{\partial}{\partial t}\left( \iiint_{CV} e\rho dV\right) + \iint_{CS} e\rho \left( \vec{v}.d\vec{S}\right) \]

The kinetic and potential energy portions are sometimes important (especially when there are large height differences) but for simplicity, I will neglect them for now. Thus, \(e\) can be replaced by \(u\).

Then, a simplified energy balance equation will look like:

\[ \Sigma\dot{Q}-P\dot{V} = \frac{\partial}{\partial t}\left( \iiint_{CV} u\rho dV\right) + \iint_{CS} u\rho \left( \vec{v}.d\vec{S}\right) \]

The last term is the energy flowing into or out of the control volume as carried by the fluid particles. For instance, in the figure above where I'm talking about the particle needing to displace existing particles to make space for itself, that new particle might also be hotter than the existing particles. So, it will effectively add energy into the pipe. This is the rightmost term above.

So, if our control volume was just a pipe, this energy could only come in or out from the ports. Then, our complicated looking integral would simplify to \(\iint_{CS} u\rho \left( \vec{v}.d\vec{S}\right)=\Sigma{m.h}_{in}-\Sigma{m.h}_{out}\).

Well done! You now know about as much as I do about how the three governing equations of fluid flow are set up. In future articles, we will be able to start formulating these equations in a format that the computer can understand. See you then!

[1]	I blame Kays and Crawford - Kays, W. M., and M. E. Crawford. "Convective Heat and Mass Transfer", McGraw-Hill, New York, 1980.