On the relative growings of a ladder
2025-01-03
Thompson's 1965 masterpiece "Calculus Made Easy" is one of the best, most enjoyable textbooks that I've ever read.
"Being myself a remarkably stupid fellow, I have had to unteach myself the difficulties, and now beg to present to my fellow fools the parts that are not hard".
A classic.
In Chapter 2, he talks about a ladder resting against a wall. As we pull the ladder away from the wall, it descends down the wall. He makes an offhand remark that as the ladder is pulled away from the wall, "the height \(y\) reached by the ladder decreases in a corresponding manner, slowly at first, but more rapidly as x becomes greater." [emphasis mine]
What a wonderful journey to go down on.
The calculations are straightforward. The length of the ladder is fixed, and x (the horizontal distance to the wall) and y (the height reached by the ladder) are related by the Pythagoras Theorem:
\[x^2 + y^2 = L^2\]L being the length of the ladder of course.
So, what happens when we pull the ladder outward? x becomes x + dx, and y becomes y + dy, but the length of the ladder itself remains unchanged.
\[(x+dx)^2 + (y+dy)^2 = L^2\]This new length must be the same as the old length. Therefore,
\[(x+dx)^2 + (y+dy)^2 = x^2 + y^2\] \[x^2+2xdx+(dx)^2 + y^2+2ydy+(dy)^2 = x^2 + y2\]Now, we neglect \((dx)^2\) and \((dy)^2\) because of Chapter 2: On different degrees of smallness. Also, \(x^2\) and \(y^2\) cancel out, as does the '2'.
\[x.dx + y.dy = 0\]Leaving,
\[dy/dx = -x/y\]Easy enough to calculate[1].
We can also check this with a real example. 5 m ladder, 4 m up the wall. Of course, that means it is 3 m away from the wall. Now, if we slide it by 0.1 cm:
\[(y+dy)^2 = 5^2 - 3.1^2\] \[(y+dy)^2 = 15.39\] \[(y+dy) = 3.923\] \[dy = 3.923-4 = -0.0769\]Which is very close to \(- x.dx/y = -0.075\). It would have been closer still had we not taken such a huge dx of 0.1 m.
Great, so far so trivial. But that throwaway remark kept eating at me. How have I lived 35 years without knowing that the ladder didn't somehow slide linearly down the wall?
Let's plot this.
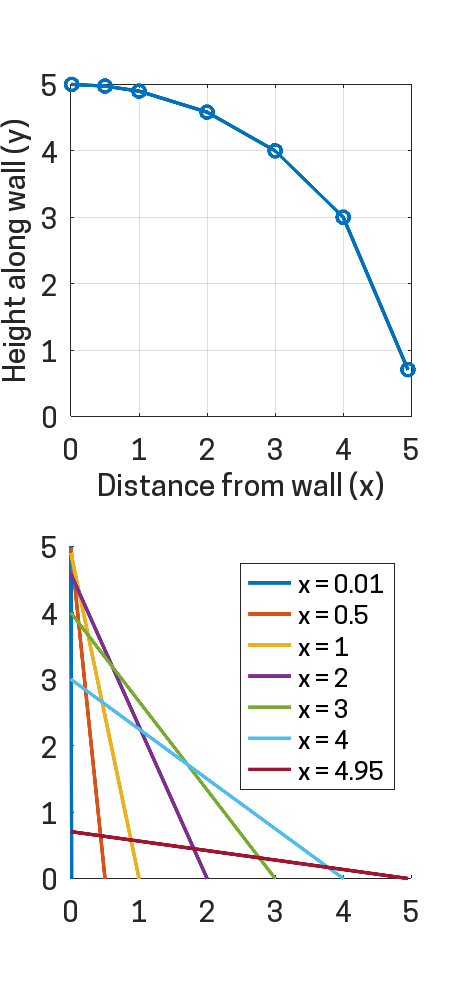
Well, I'll be damned.
When the ladder is nigh-on vertical against the wall (x = 0.01), the height along the wall is virtually the entire length of the ladder. Then, as we start pulling it, almost nothing happens at first. After we've pulled the ladder a whole metre away, we're still only 0.1 metres down the wall. Heck, after we're well past halfway pulling the ladder apart, at x = 3 m, we're only just beginning to lose the first metre of height (y = 4 m). The full results are below:
| x | y |
|---|---|
| 0.01 | 5.00 |
| 0.50 | 4.97 |
| 1.00 | 4.90 |
| 2.00 | 4.58 |
| 3.00 | 4.00 |
| 4.00 | 3.00 |
| 4.95 | 0.70 |
Remarkable. Now, dy/dx depends on x. So, the larger the x becomes, the larger the rate of change becomes. But it also depends on y, so the smaller y becomes, the larger still becomes the rate of change. Double whammy! Below is the plot of dy/dx plotted against x.
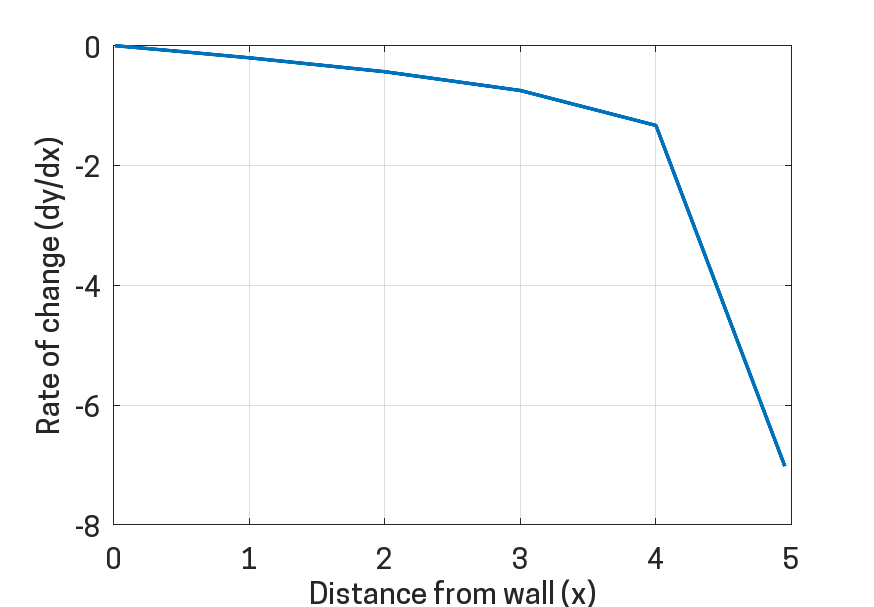
The effect is much more dramatic than I imagined. Even going from three metres to four metres away from the wall, we still only lost one more metre in height. But in the last 0.95 metres, we lose nearly all of our length. This is confirmed by the dy/dx plot, with the rate of change skyrocketing as we careen towards the end.
What was the point of this post? Nothing. Just an interesting thought exercise.
Here's the code for the plots. I generated it using Octave, because I can't figure out how to run Matlab on Wayland.
clc
clear
L = 5;
x = [0.01 0.5 1 2 3 4 4.95];
y = sqrt(L.^2 - x.^2);
dydx = -x./y
set(0,'defaultlinelinewidth',2);
set(0,'defaulttextfontname','Cooper Hewitt Medium');
set(0,'defaultaxesfontname','Cooper Hewitt Medium');
set(0,'DefaulttextFontSize',13);
set(0,'DefaultaxesFontSize',13);
aoeu = figure;
set(gcf,'Units','centimeters','Position',[1, 1, 30, 20]);
subplot(2,1,1);
h = plot(x,y,'-o');
xlabel('Distance from wall (x)');
ylabel('Height along wall (y)');
xlim([0, 5]);
ylim([0, 5]);
grid on
subplot(2,1,2)
hold on
for i = 1:length(x)
str = sprintf('x = %d',x(i));
plot([x(i),0],[0,y(i)],'DisplayName',str);
end
legend
figure
plot(x,dydx)
xlabel('Distance from wall (x)');
ylabel('Rate of change (dy/dx)');
grid on
box on| [1] | In the book Thompson includes a negative sign x+dx ⇒ y-dy, but then, at the last minute, pulls the rug from under us and corrects himself, giving dy/dx = -x/y. But, if he'd assumed y-dy, he should have gotten +x/y. |